Water Drop Linkage: Modeling and Simulation Using Gnuplot

YouTube

Modeling of water drop linkage

Find the coordinates of the points $\mathrm{A}$ and $\mathrm{C}$

Let \[\mathrm{OA}=\mathrm{AB}=a,\ \mathrm{OB}=\mathrm{OC}=2a,\ \mathrm{AP}=3a\] Then \begin{eqnarray} \overrightarrow{\mathrm{OA}} &=& \begin{bmatrix}-a\sin\theta \\ a\cos\theta\end{bmatrix}\\ \overrightarrow{\mathrm{OC}} &=&\begin{bmatrix}0 \\ -2a\end{bmatrix} \end{eqnarray}

Find the coordinates of the point $\mathrm{B}$

\begin{equation}\overrightarrow{\mathrm{OB}}=\overrightarrow{\mathrm{OC}}+\overrightarrow{\mathrm{CB}}=\begin{bmatrix}-4a\cos\alpha\sin\alpha\\-4a\cos^2\alpha\end{bmatrix}\end{equation} where \begin{align} l&=a\sqrt{5+4\cos\theta}\\ \cos\alpha &= \frac{l^2+3a^2}{4al} \\ \sin\alpha &= \begin{cases}\ \ \ \sqrt{1-\cos^2\alpha}\ \ (\ \ \ \ 0^\circ\leq\theta\leq 180^\circ)\\ -\sqrt{1-\cos^2\alpha}\ \ (180^\circ < \theta < 360^\circ)\end{cases} \end{align}

Find the coordinates of the point $\mathrm{P}$

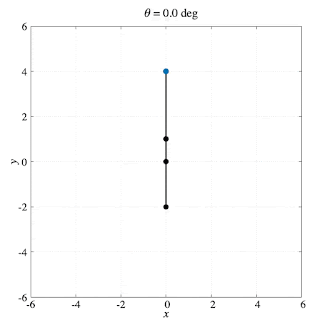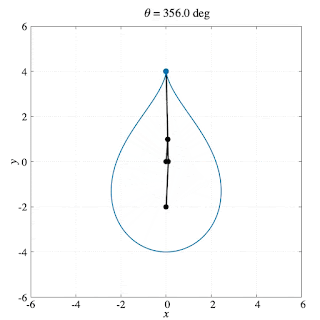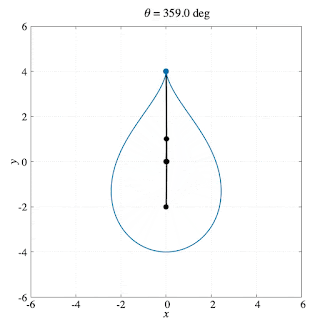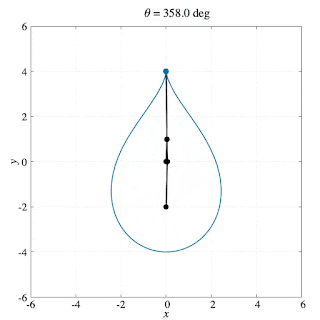
\begin{align}\overrightarrow{\mathrm{OP}}&=\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{AP}}= \overrightarrow{\mathrm{OA}}+3\overrightarrow{\mathrm{BA}}= 4\overrightarrow{\mathrm{OA}}-3\overrightarrow{\mathrm{OB}}\\ \therefore\overrightarrow{\mathrm{OP}} &= \begin{bmatrix}-4a\sin\theta+12a\cos\alpha\sin\alpha \\ 4a\cos\theta+12a\cos^2\alpha\end{bmatrix}\end{align}

Simulation [gnuplot]

Source code (PLT file)

Output (PNG file → GIF file)

Referece

The link mechanism in the video is based on the following tweet by Keishiro Ueki.
▶︎ https://twitter.com/ChocoLinkage/status/1399198044122271746?s=20