YouTube
Simulation [gnuplot]
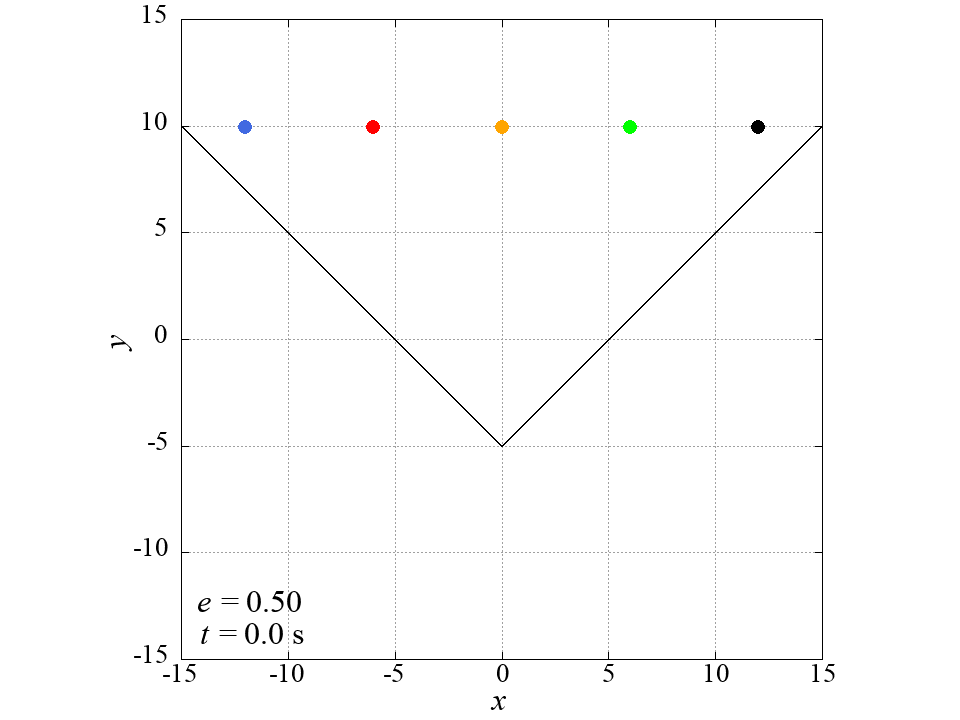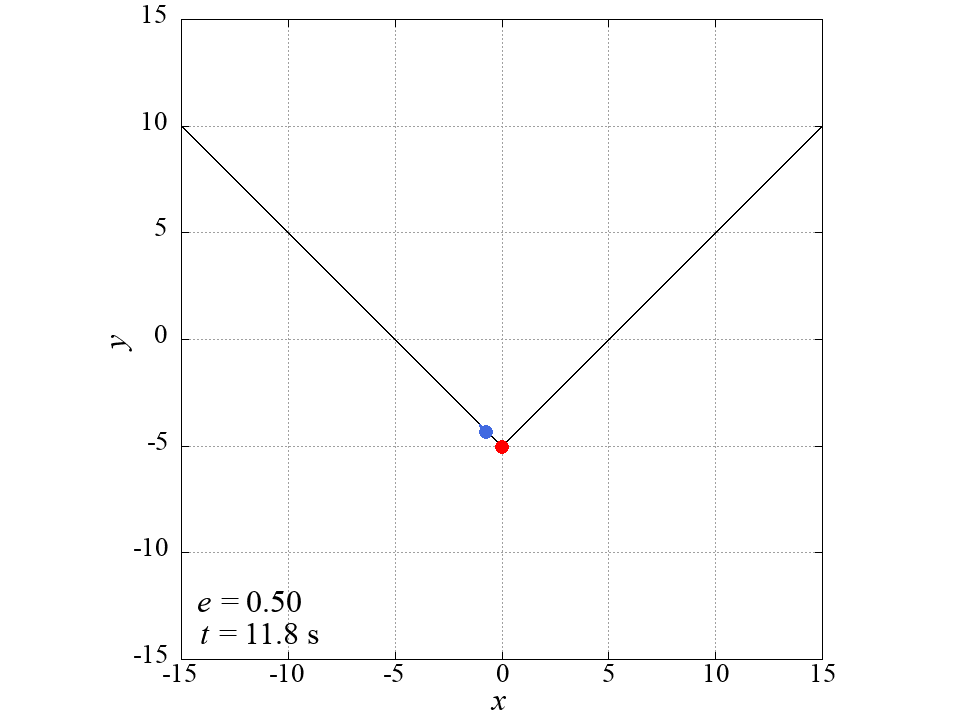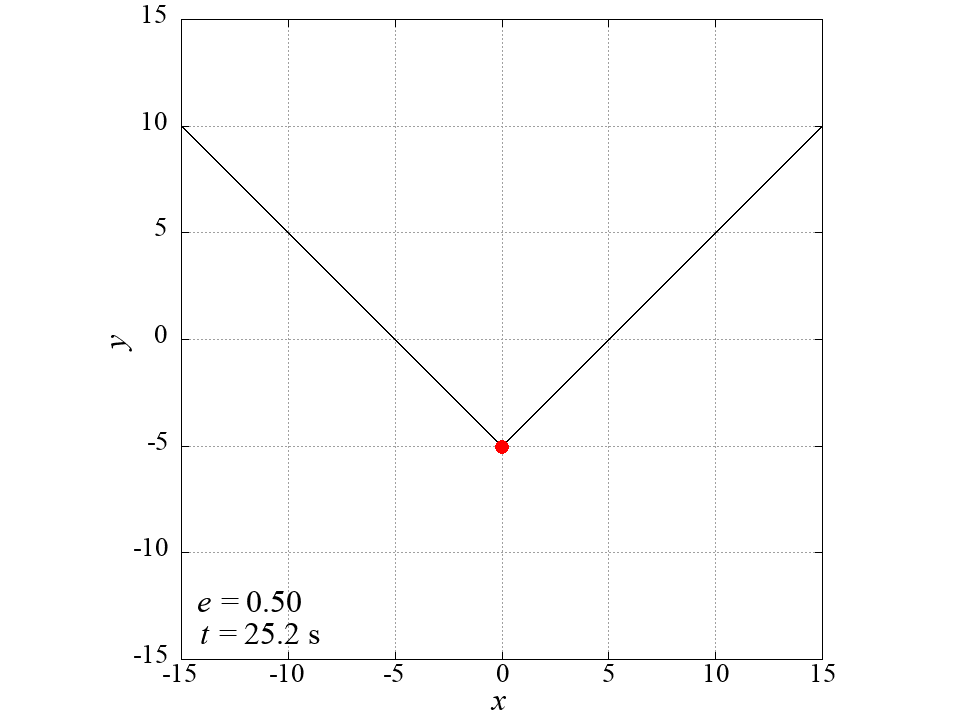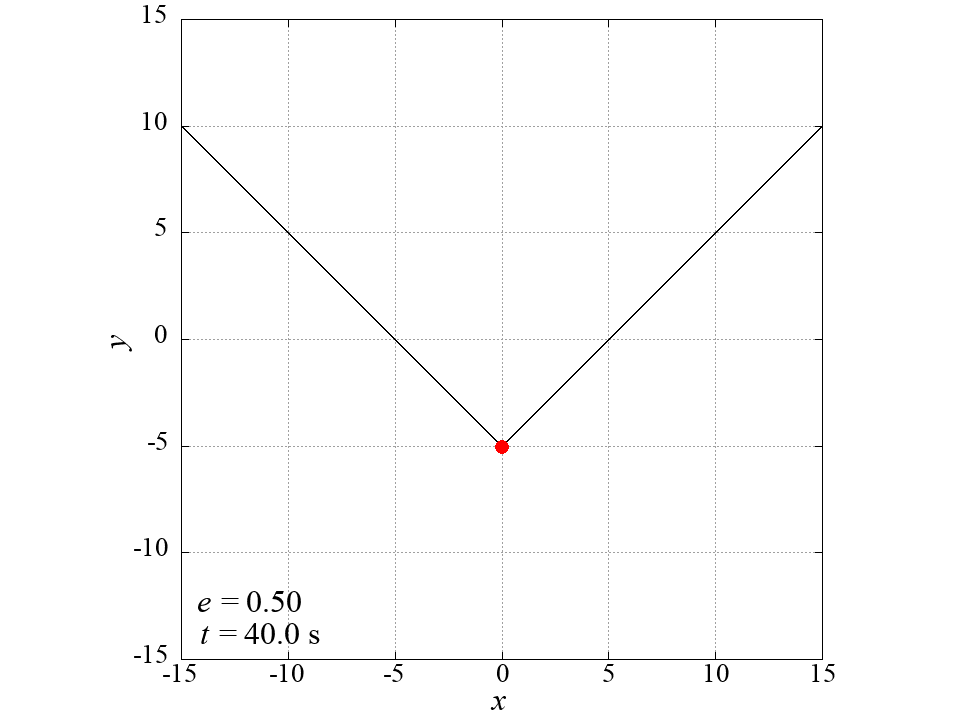
Model of a Bouncing Ball
Impulse-momentum theorem \begin{eqnarray} \label{eq:im3} m\boldsymbol{v}'=m\boldsymbol{v}+\boldsymbol{I}=m\boldsymbol{v}+I\boldsymbol{n} \end{eqnarray} Collision \begin{eqnarray} \left|\boldsymbol{v}'\cdot\boldsymbol{n}\right|=e\left|\boldsymbol{v}\cdot\boldsymbol{n}\right| \end{eqnarray} Calculating I \begin{eqnarray} I &=& \left| \left(m\boldsymbol{v}'\right) \cdot \boldsymbol{n} \right| + \left| \left(m\boldsymbol{v}\right) \cdot \boldsymbol{n} \right| \nonumber\\ &=& m\left(\left|\boldsymbol{v}' \cdot \boldsymbol{n} \right| + \left| \boldsymbol{v} \cdot \boldsymbol{n} \right|\right) \nonumber\\ &=& m\left(e\left|\boldsymbol{v}\cdot\boldsymbol{n}\right|+\left|\boldsymbol{v}\cdot\boldsymbol{n}\right|\right) \nonumber\\ &=& -m\left(e+1\right) \left( \boldsymbol{v} \cdot \boldsymbol{n} \right) \label{eq:I} \end{eqnarray} Velocity after the collision (inserting (\ref{eq:I}) into (\ref{eq:im})) \begin{eqnarray} \boldsymbol{v}'=\boldsymbol{v}-(e+1)\left(\boldsymbol{v}\cdot\boldsymbol{n}\right)\boldsymbol{n} \end{eqnarray}
Wall function \begin{equation} W(x, y)=y-f(x) \end{equation} Inequality constraint \begin{equation} W(x, y)\geq 0 \end{equation} Unit normal vector \begin{equation} \boldsymbol{n}=\frac{\nabla W}{\left|\nabla W\right|} \end{equation} Collision detection \begin{equation} \boldsymbol{v}'=\boldsymbol{v}-\left(e+1\right)\left(\boldsymbol{v}\cdot \frac{\nabla W}{\left|\nabla W\right|}\right)\frac{\nabla W}{\left|\nabla W\right|} \end{equation}
Case 1: $f(x)=\left(\frac{x}{7}\right)^2-13$
PLT file ①
# Setting --------------------
reset
set term gif animate delay 5 size 1280, 720
set output"ball_fx.gif"
set nokey
set sample 10000
set xr[-35:35]
set yr[-15:15]
set xl "{/TimesNewRoman:Italic=24 x}"
set yl "{/TimesNewRoman:Italic=24 y}"
set tics font 'Times New Roman,20'
set xtics 5
set ytics 5
set size ratio -1 # ratio = yrange / xrange
set grid
N = 5
array x[N]
array y[N]
array vx[N]
array vy[N]
array c[N] = ["royalblue", "red", "orange", "green", "black"]
# Parameter --------------------
r = 0.3 # Radius of the ball
g = 9.8 # Gravitational acceleration
dis = 500 # Start to disappear
e = 0.95 # Elasticity coefficient
dt = 0.001 # Time step
dh = dt/6
cut = 80 # Decimation
ep = 1e-4 # for collision detection
time1 = 2 # Stop time4
lim1 = time1/dt/cut
time2 = 40 # Time limit40
lim2 = time2/dt
# Functions --------------------
# Wall
g(x) = x**2
f(x) = g(x/7.)-13.
W(x, y) = y-f(x)
# Partial derivative of f(x)
Wx(x) = -(f(x-2*dt)-8*f(x-dt)+8*f(x+dt)-f(x+2*dt)) / (12*dt) # 4th order central difference formula
Wy(y) = 1
# n = (fx, fy) / sqrt(fx^2+fy^2)
d(x, y) = sqrt(x**2+y**2)
nx(x, y) = Wx(x)/d(Wx(x), Wy(y))
ny(x, y) = Wy(y)/d(Wx(x), Wy(y))
# Inner product of v and n
vn(x,y,vx,vy) = vx*nx(x,y)+vy*ny(x,y)
I(x,y,vx,vy) = -(1+e)*vn(x,y,vx,vy)
# Equations of Motion
rk1(x,y,vx,vy) = vx # dx/dt
rk2(x,y,vx,vy) = vy # dy/dt
rk3(x,y,vx,vy) = 0 # dvx/dt
rk4(x,y,vx,vy) = -g # dvy/dt
# 4th order Runge-Kutta (Define RK_i(x, y, vx, vy))
do for[i=1:4]{
RKi = "RK"
rki = "rk".sprintf("%d", i)
RKi = RKi.sprintf("%d(x, y, vx, vy) = (\
k1 = %s(x, y, vx, vy),\
k2 = %s(x + dt*k1/2., y + dt*k1/2., vx + dt*k1/2., vy + dt*k1/2.),\
k3 = %s(x + dt*k2/2., y + dt*k2/2., vx + dt*k2/2., vy + dt*k2/2.),\
k4 = %s(x + dt*k3, y + dt*k3, vx + dt*k3, vy + dt*k3),\
dh * (k1 + 2*k2 + 2*k3 + k4))", i, rki, rki, rki, rki)
eval RKi
}
# Label of displaying parameters
# Elastic
e(e) = sprintf("{/TimesNewRoman:Italic e} = %.2f", e)
# Time
Time(t) = sprintf("{/TimesNewRoman:Italic t} = %.1f s", t)
# Plot --------------------
# Initiate value
t = 0.0 # Time
do for[j=1:N]{
x[j] = 13.*(j-3)-2 # Position
y[j] = 10.
vx[j] = 0. # Velocity
vy[j] = 0.
}
# Draw initial state for lim1 steps
do for[i=1:lim1]{
# Time
set label 1 Time(t) font 'Times New Roman, 24' at graph 0.03, 0.03
set label 2 e(e) font 'Times New Roman, 24' at graph 0.023, 0.08
# Ball
do for[j=1:N]{
set object j+1 circle at x[j], y[j] size r fc rgb c[j] fs solid front
}
plot f(x) lc rgb 'black'
}
# Update
do for[i=1:lim2]{
# Time
t = t + dt
set label 1 Time(t)
# Balls
do for[j=1:N]{
# 4th order Runge-Kutta
tmp_x = x[j] + RK1(x[j], y[j], vx[j], vy[j])
tmp_y = y[j] + RK2(x[j], y[j], vx[j], vy[j])
tmp_vx = vx[j] + RK3(x[j], y[j], vx[j], vy[j])
tmp_vy = vy[j] + RK4(x[j], y[j], vx[j], vy[j])
# Collision detection
if(W(x[j], y[j]) >= 0 && W(tmp_x, tmp_y) < 0){
# vec = x_[i+1] - x_[i]
vec_x = tmp_x - x[j]
vec_y = tmp_y - y[j]
nor_v = d(vec_x, vec_y)
# Find collision point
while(W(x[j], y[j]) >= 0){
x[j] = x[j] + vec_x / nor_v * ep
y[j] = y[j] + vec_y / nor_v * ep
}
x[j] = x[j] - vec_x / nor_v * ep
y[j] = y[j] - vec_y / nor_v * ep
# Calculate bounce direction
size = d(tmp_x-x[j], tmp_y-y[j])
tmp_x = x[j] - (1+e) * size * vn(x[j],y[j],vec_x,vec_y) / nor_v * nx(x[j], y[j])
tmp_y = y[j] - (1+e) * size * vn(x[j],y[j],vec_x,vec_y) / nor_v * ny(x[j], y[j])
# Collision
tmp_vx = vx[j] + I(x[j], y[j], vx[j], vy[j]) * nx(x[j], y[j])
tmp_vy = vy[j] + I(x[j], y[j], vx[j], vy[j]) * ny(x[j], y[j])
}
# Update position and velocity of a ball
x[j] = tmp_x
y[j] = tmp_y
vx[j] = tmp_vx
vy[j] = tmp_vy
# Draw a ball
set object N*i+j circ at x[j], y[j] size r fc rgb c[j] fs solid front
set object N*(i-1)+j circ size r*0.01 # Old ball turns smaller
# Start to disappear
if(i>=dis){
unset object N*(i-dis)+j
}
}
# Decimate and draw
if(i%cut==0){
replot
}
}
set out
GIF file ①
$e=0.95$
Case 2: $f(x)=\left|x \right|-5$
GIF file ②
$e=1.00$
Case 3: $f(x) = \frac{x^2}{40}+\cos x-10$
GIF file ③
$e=0.95$
Case 4: $f(x)= \frac{3}{4}x\sin\left(\frac{x^2}{10}+\frac{2}{5}\pi\right)$
GIF file ④
$e=0.95$
Extra
Fall from a non-differentiable point $(f(x)=\left|x \right|-5)$
e=0.50
e=0.80
