Peaucellier–Lipkin Linkage [gnuplot]

YouTube

Formulation

Find the coordinates of all joints

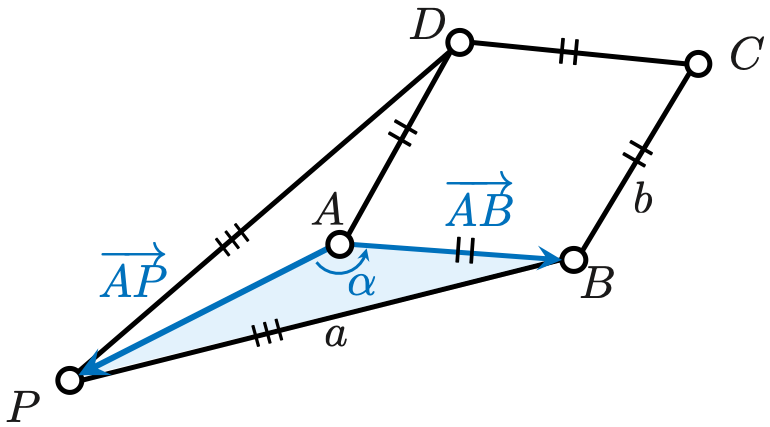
\begin{eqnarray*} OA=OP=r\\ PB=PD=a\\ AB=BC=CD=DA=b \end{eqnarray*}

Joints $A$ and $P$

\begin{equation*} \v{OA} = \begin{bmatrix}r\cos\theta\\r\sin\theta\end{bmatrix},\ \ \v{OP} = \begin{bmatrix}-r\\0\end{bmatrix} \end{equation*}

Joint $B$

\begin{eqnarray*} \v{OB} &=& \v{OA}+\v{AB}&=&\v{OA}+b\bm{R}(\alpha)\frac{\v{AP}}{\left|\v{AP}\right|} \end{eqnarray*} where \begin{eqnarray*} \begin{cases} \bm{R}(\theta)=\begin{bmatrix}\cos\theta & -\sin\theta\\ \sin\theta & \cos\theta\end{bmatrix}\\ \alpha = \arccos\left(\frac{AP^2+b^2-a^2}{2\cdot AP\cdot b}\right) \end{cases} \end{eqnarray*}

Joint $D$

\begin{eqnarray*} \v{OD} &=& \v{OA}+\v{AD}&=&\v{OA}+b\bm{R}(-\alpha)\frac{\v{AP}}{\left|\v{AP}\right|} \end{eqnarray*}

Joint $C$

\begin{eqnarray*} \v{OC} &=& \v{OA}+\v{AC} = \v{OA}+\v{AB}+\v{AD}\\ &=&\v{OA} + b\left[\bm{R}(\alpha)+\bm{R}(-\alpha)\right]\frac{\v{AP}}{\left|\v{AP}\right|}\\ &=& \begin{bmatrix} \frac{a^2-b^2}{2r}-r\\ \frac{a^2-b^2}{2r}\tan\frac{\theta}{2} \end{bmatrix} \end{eqnarray*} Since $C_x$ is constant, this mechanism generates exact straight-line motion.

Finding the maximum value of $C_y(\theta)$

The value of $\theta$ giving the maximum value of $C_y(\theta)$

\begin{equation} \theta_{\mathrm{max}}=2\beta,\ \mathrm{where}\ \ \beta=\arccos\left(\frac{a-b}{2r}\right) \end{equation}

The maximum value of $C_y(\theta)$

\begin{equation} C_y(\theta_{\mathrm{max}})=(a+b)\sin\beta \end{equation}

Simulation [gnuplot]

Source code (PLT file)

Output (PNG file → GIF file)

Animation 1 : Drawing only linkage mechanism

Animation 2 : Drawing not only linkage mechanism but also locus

Examples pf parameter sets

Determining the incidence of the red line and blue circle \begin{eqnarray*} C_x\gtreqqless r&\ \Longleftrightarrow\ & \frac{a^2-b^2}{2r}-r \gtreqqless r\\ &\ \Longleftrightarrow\ & a^2 \gtreqqless b^2+(2r)^2\ \ \ \ (\because r>0) \end{eqnarray*}

Condition 1 : $C_x > r\ \ (r=4,\ a=9,\ b=2)$

Condition 2 : $C_x = r\ \ (r=2,\ a=5,\ b=3)$

Condition 3 : $C_x < r\ \ (r=3,\ a=6,\ b=3)$

Note : get dashed lines in png terminal

PNG terminal don't support dashed lines. On the other hand, pngcairo terminal support dashed lines, but is disabled by default ^[1][2]. To enable it and using it in different curves, use:

set terminal pngcairo dashed

If you want to get dashed lines in png terminal, you can get them by setting linetype '0'. 'test.png' is outputted by the following code ^[3].

set output "test.png"
set terminal png truecolor enhanced
test

References

1. ^ Gnuplot | #27 How to get dashed line or arrow? - Facebook
2. ^ gnuplot png output doesn't plot dashed/dotted lines - Stack Overflow
3. ^ Create a list of points, lines, and colors - Shingo Yonezawa Home Page (in Japanese)

External links

▶︎ Peaucellier–Lipkin linkage - Wikipedia