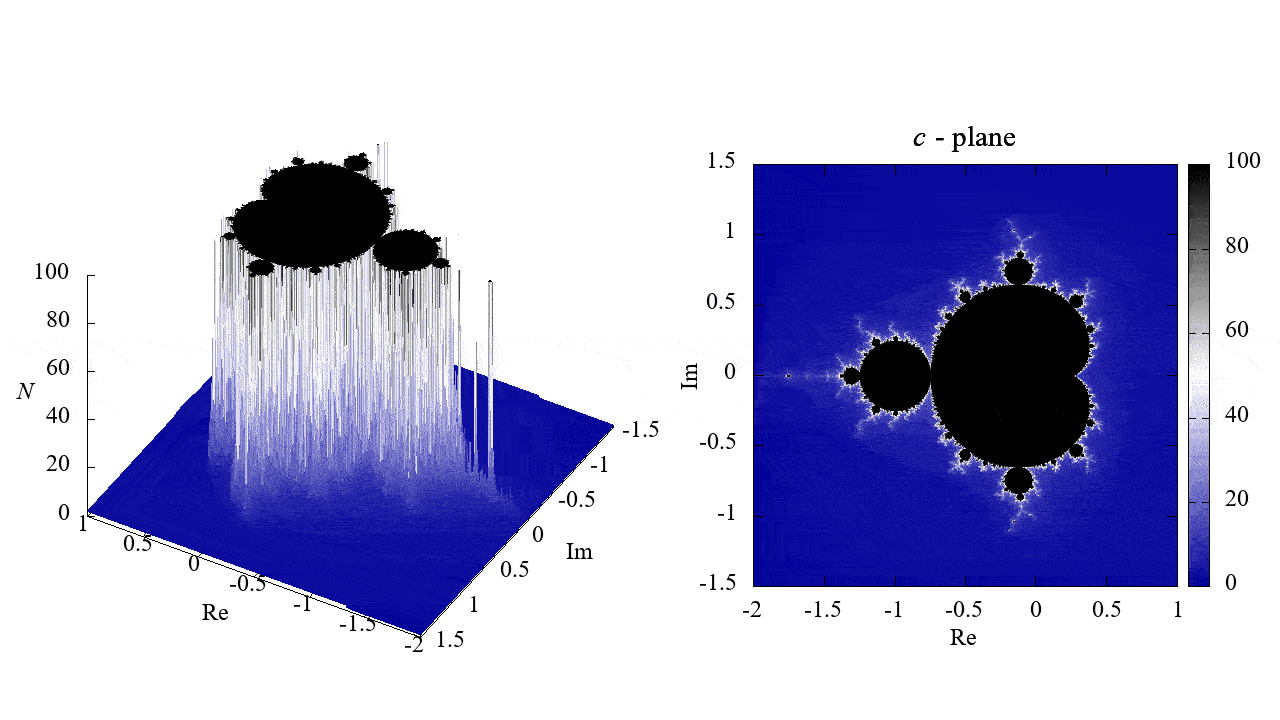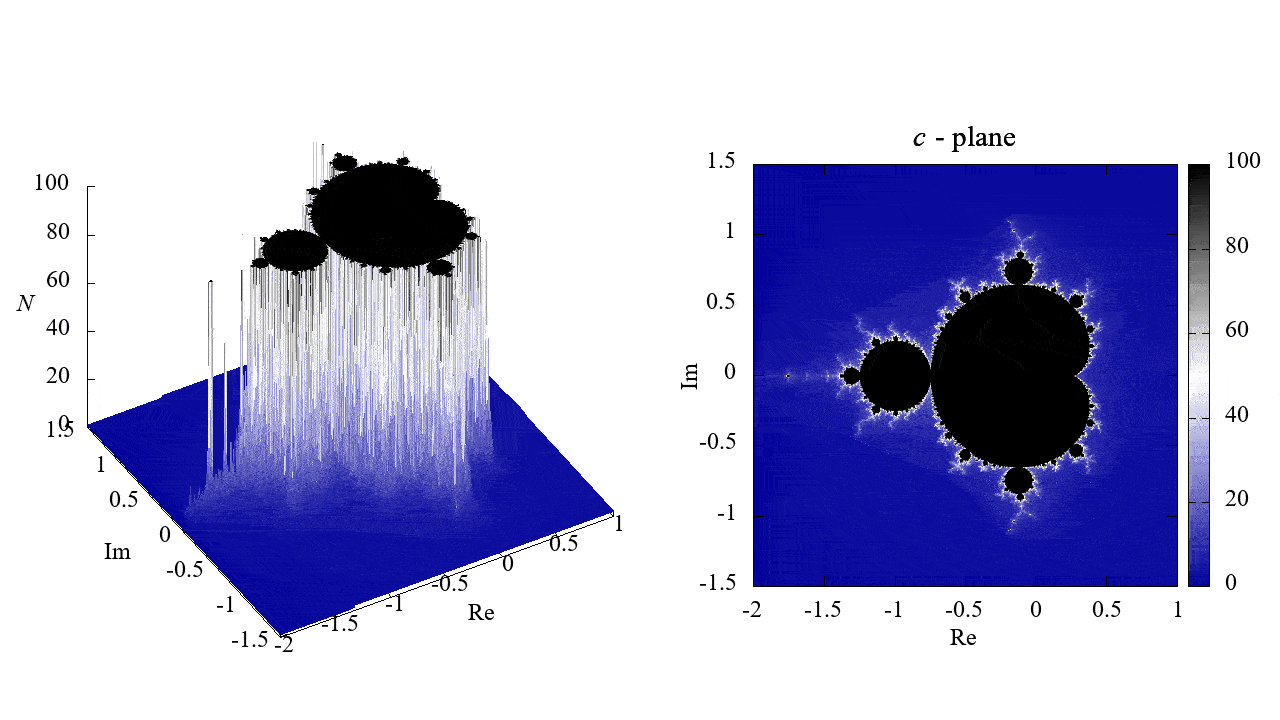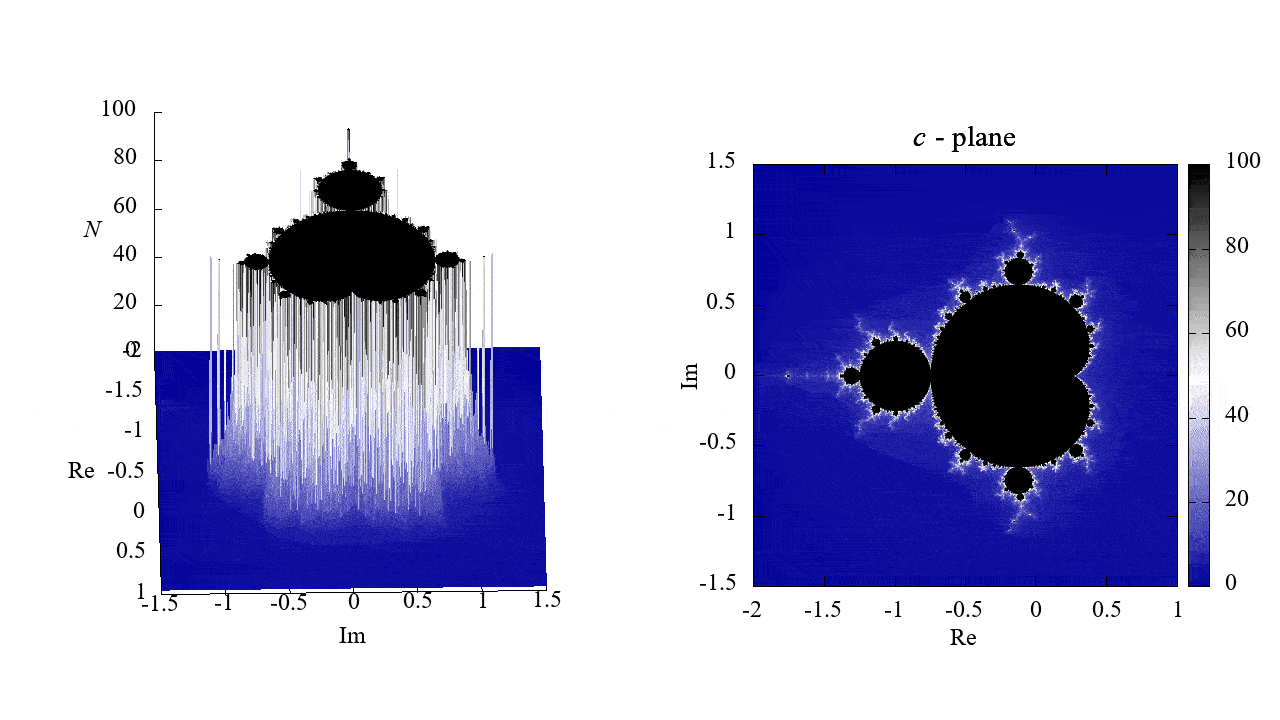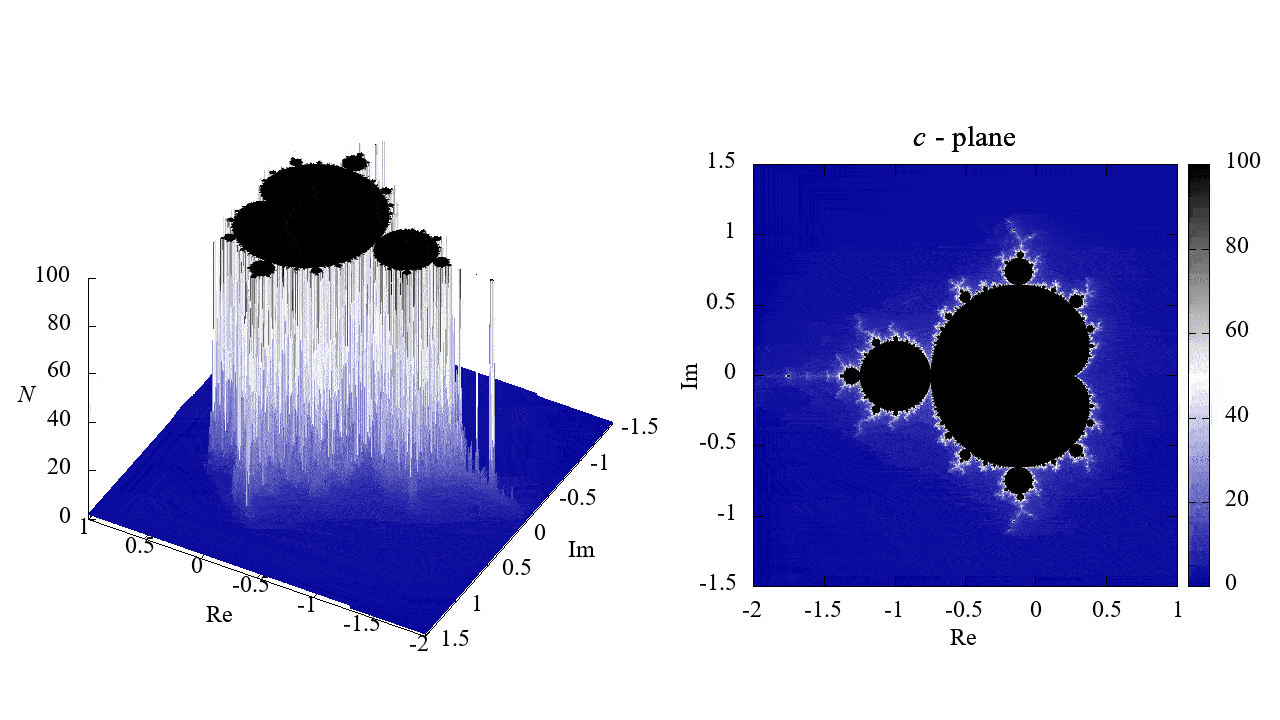
Mandelbrot set
mandelbrot.plt
mandelbrot.gif
Julia set
julia.plt
julia.gif
Multiplot Mandelbrot / Julia set
multiplot_man_jul.plt
multiplot_path=cardioid.gif
Other examples of palette
set palette cubehelix start 1 cycles -5 saturation 3 positive # cube (YouTube 2:20) set palette defined(0"black", 1"red", 2"white", 3"black") # black (YouTube 4:28)
multiplot_path=circle.gif
[13th line] palette: black[66th line] obj 1 : light-green



No comments:
Post a Comment